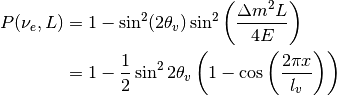Vacuum Oscillation

Schrodinger equation is

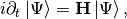
i\partial_t \ket{\Psi} = \mathbf H \ket{\Psi},

where for relativistic neutrinos, the energy is

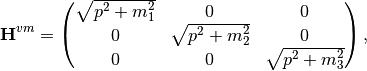
\mathbf H^{vm} &= \begin{pmatrix}\sqrt{p^2 + m_1^2} & 0 & 0 \\ 0& \sqrt{p^2 + m_2^2} & 0 \\ 0 & 0 & \sqrt{p^2 + m_3^2} \end{pmatrix},

in which the energy terms are simplified using the relativistic condition

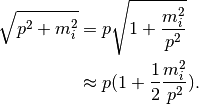
\sqrt{p^2+m_i^2} & = p\sqrt{1 + \frac{m_i^2}{p^2}} \\ &\approx p(1 + \frac{1}{2} \frac{m_i^2}{p^2}).

So Called Decoherence

Here we assume that they all have the same energy but different mass. The thing is we assume they have the same velocity since the mass is very small. To have an idea of the velocity difference, we can calculate the distance travelled by another neutrino in the frame of one neutrino.

Assuming the mass of a neutrino is 1eV with energy 10MeV, we will get a speed of 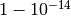1-10^{-14} c. This 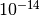10^{-14} c will make a difference about 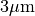3\mu\mathrm{ m} in 1s.

Will decoherence happen due to this? For high energy neutrinos this won’t be a problem however for low energy neutrinos this will definitely cause a problem for the wave function approach.Because the different mass eigenstates will become decoherent gradually along the path.

A estimation of the decoherence length is

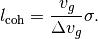
l_{\mathrm{coh}}=\frac{v_g}{\Delta v_g}\sigma.

To obtain the relation,

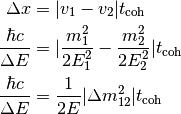
\Delta x &= \lvert v_1 - v_2 \rvert t_{\mathrm{coh}}\\ \frac{\hbar c}{\Delta E} & = \lvert \frac{m_1^2}{2E_1^2} - \frac{m_2^2}{2E_2^2} \rvert t_{\mathrm{coh}} \\ \frac{\hbar c}{\Delta E} & = \frac{1}{2E}\lvert \Delta m_{12}^2 \rvert t_{\mathrm{coh}}

It should be made clear that this is not really decoherence but in the view of wave packet formalism different propagation eigenstates will be far away from each other. As long as we put them together again we can overlap and oscillate again. No quantum decoherence is happening at all.

In general the flavor eigenstates are the mixing of the mass eigenstates with a unitary matrix $mathbf U$, that is

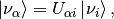
\ket{\nu_{\alpha}} = U_{\alpha i} \ket{\nu_i},

where the 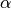\alpha s are indices for flavor states while the $i$s are indices for mass eigenstates.

To find out the equation of motion for flavor states, plugin in the initary tranformation,

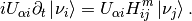
i U_{\alpha i} \partial_t \ket{\nu_i} = U_{\alpha i} H^m_{ij} \ket{\nu_j}.

We use index :math:{}^{vm}$ for representation of Hamiltonian in mass eigenstates in vacuum oscillations. Applying the unitary condition of the transformation,

\mathbf I = \mathbf {U^\dagger} \mathbf U,

I get

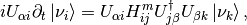
i U_{\alpha i} \partial_t \ket{\nu_i} = U_{\alpha i} H^m_{i j} {U^\dagger_{j\beta}} U_{\beta k} \ket{\nu_k},

which is simplified to

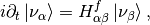
i \partial_t \ket{\nu_\alpha} = H^f_{\alpha \beta} \ket{\nu_{\beta}},

since the transformation is time independent.

The new Hamiltonian in the representations of flavor eigenstates reads

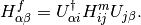
H^f_{\alpha\beta} = U^\dagger_{\alpha i} H^m_{ij} U_{j\beta}.

Survival Problem

The neutrino states at any time can be written as

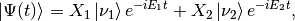
\ket{\Psi(t)} = X_1 \ket{\nu_1 } e^{-i E_1 t}+ X_2 \ket{ \nu_2 } e^{-i E_2 t},

where 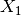X_1 and $X_2$ are the initial conditions which are determined using the neutrino initial states.

Survival probalility is the squrare of the projection on an flavor eigenstate,

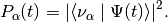
P_{\alpha}(t) = \lvert \braket{\nu_{\alpha}}{\Psi(t)} \rvert^2.

The calculation of this expression requires our knowledge of the relation between mass eigenstates and flavor eigenstates which we have already found out.

Recall that the transformation between flavor and mass states is

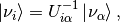
\ket{\nu_i} = U^{-1}_{i\alpha} \ket{\nu_\alpha},

which leads to the inner product of mass eigenstates and flavor eigenstates,

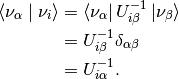
\braket{\nu_\alpha}{\nu_i} &= \bra{\nu_\alpha} U^{-1}_{i\beta} \ket{\nu_\beta} \\ & = U^{-1}_{i\beta}\delta_{\alpha\beta} \\ & = U^{-1}_{i\alpha}.

The survival probability becomes

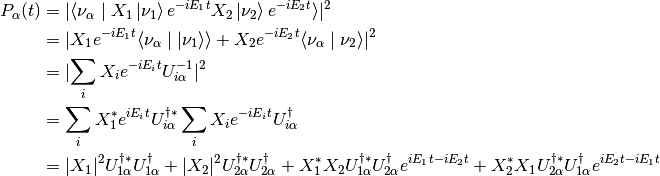
P_\alpha (t) &= \lvert \braket{\nu_\alpha}{ X_1 \ket{\nu_1 } e^{-i E_1 t} X_2 \ket{ \nu_2 } e^{-i E_2 t} } \rvert^2 \\ & = \lvert X_1 e^{-i E_1 t} \braket{\nu_\alpha}{\ket{\nu_1} } + X_2 e^{-i E_2 t} \braket{ \nu_\alpha }{ \nu_2 } \rvert^2 \\ & = \lvert \sum_i X_i e^{-i E_i t} U^{-1}_{i \alpha} \rvert ^2 \\ & = \sum_i X_1^* e^{iE_i t} U^{\dagger *}_{i\alpha} \sum_i X_i e^{-i E_i t} U^\dagger_{i \alpha} \\ & = \lvert X_1 \rvert^2 U^{\dagger * } _ {1\alpha} U^\dagger_{1\alpha} + \lvert X_2 \rvert^2 U^{\dagger * } _ {2\alpha} U^\dagger_{2\alpha} + X_1^* X_2 U^{\dagger * }_{1\alpha} U^\dagger_{2\alpha} e^{i E_1 t - i E_2 t} + X_2^* X_1 U^{\dagger * }_{2\alpha} U^\dagger_{1\alpha} e^{i E_2 t - i E_1 t}

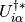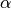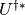U^{\dagger *}_{i\alpha} stands for the $i$th row and the \alpha th column of the matrix U^{\dagger *}.

Two Flavor States

Suppose the neutrinos are prepared in electron flavor initially, the survival probability of electron flavor neutrinos is calculated using the result I get previously.

Electron neutrinos are the lighter ones, then I have {}_a = {}_e and denote {}_b={}_x.

Meaning of Mixing

In the small mixing angle limit,

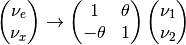
\begin{pmatrix}\nu_e \\ \nu_x\end{pmatrix} \to \begin{pmatrix} 1 & \theta \\ -\theta & 1 \end{pmatrix} \begin{pmatrix}\nu_1 \\ \nu_2\end{pmatrix}

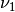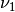which is very close to an identity matrix. This implies that electron neutrino is more like mass eigenstate \nu_1 . By \nu_1 we mean the state with energy 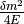\frac{ \delta m^2 }{4E} in vacuum.

In fact the dynamics of the system is very easily solved without dive into the math. Suppose we have 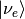\ket{\nu_e} initially, which is

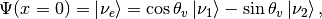
\Psi(x=0)=\ket{\nu_e} = \cos \theta_v \ket{\nu_1} - \sin \theta_v \ket{\nu_2},

the state of the system at distance 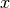x is directly written down

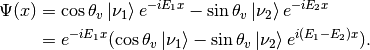
\Psi(x) &= \cos \theta_v \ket{\nu_1} e^{-i E_1 x} - \sin \theta_v \ket{\nu_2} e^{-i E_2 x} \\ &= e^{-i E_1 x}( \cos \theta_v \ket{\nu_1} - \sin \theta_v \ket{\nu_2} e^{i(E_1 - E_2) x}).

Since a global phase doesn’t change the detection, we write the state as

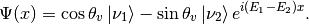
\Psi(x) = \cos \theta_v \ket{\nu_1} - \sin \theta_v \ket{\nu_2} e^{i(E_1 - E_2) x} .

Notice that the period of the expression is

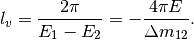
l_v = \frac{2\pi}{E_1 - E_2} = - \frac{4\pi E}{\Delta m_{12}}.

Then the state becomes

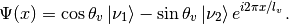
\Psi(x) = \cos \theta_v \ket{\nu_1} - \sin \theta_v \ket{\nu_2} e^{i2\pi x/l_v} .

The survival probability for electron neutrinos is

P(\nu_e,L) &= 1-\sin^2(2\theta_v)\sin^2\left( \frac{\Delta m^2 L}{4E} \right) \\ &= 1- \frac{1}{2}\sin^2 2\theta_v \left(1- \cos\left( \frac{2\pi x}{l_v} \right) \right)

Refs and Notes